The Basics
Datums are discussed here at two levels:
- The Basics
- Datums Explained in More Detail
The content of these two is very similar, but as their titles suggest, they supply different levels of information. As Datums is a ‘jargon rich’ discipline it is recommended that you read this Section first.
As with all the Modules in this package, ICSM is trying to explain often complex situations using very simple language. In the case of Datums this is particularly true. Once you understand the principles being outlined in these two sections it is recommended that you use the hyperlinks to more complex sites if you wish to better understand the intricacies associated with datums.
What is a Datum and how is it Different to a Projection?
This confuses many people. In simple terms:
A datum is a system which allows the location of latitudes and longitudes (and heights) to be identified onto the surface of the Earth - ie onto the surface of a ’round’ object.
The basic 
mathematical/geometric principle which is used is that:
» mathematically a ’round’ surface (a modified sphere) is created which represents the surface of the Earth
» from here calculations are made to fit this mathematical model to the surface of the Earth - firstly the Equator, then North and South Poles and then lines of latitude and longitude.
Refer to the section on the Earth’s coordinate system.
Because there are different ways to fit the mathematical model to the surface of the Earth, there are many different datums. Also, in the modern digital era, techniques have vastly improved and many modern datum are very similar to each other. However, also in this modern digital era, people like to know locations precisely so even a small difference may be significant.
A projection is a process which uses the latitude and longitude which has already been ‘drawn’ on the surface of the Earth using a datum, to then be ‘drawn’ onto a ‘flat piece of paper’ - called a map.
See the section on Projections for more information about projection methodologies.
Naming Datums and Projections
There are many different datums and projections in existence. To ensure that these can be easily identified each version of a datum or projection is given a unique name:
For datums this is usually a regional/functional description and a date for when it was last up–dated - for example:
- the Australian Geodetic Datum which was created in 1966 and updated in1984 is variably described as AGD66, AGD84 or just AGD
- the International Terrestrial Reference frame is described as ITRF - this has versions which were created in 1994, 1996, 1997, 2000 and 2005
- the United States Defence Department developed the World Geodetic System 1984 or WGS84 – this is used by GPS satellite navigation systems and on most hydrographic charts
For projections names include:
» the person(s) who developed it (eg Mercator); or
» aspects of the projection (eg Conic); or
» a combination of the two (eg Lambert Conformal Conic).
About the Geometry of Datums
In order to calculate where latitudes and longitudes occur on the surface of the Earth a number of fundamental geometric concepts and practices need to be applied. In simple terms these include:
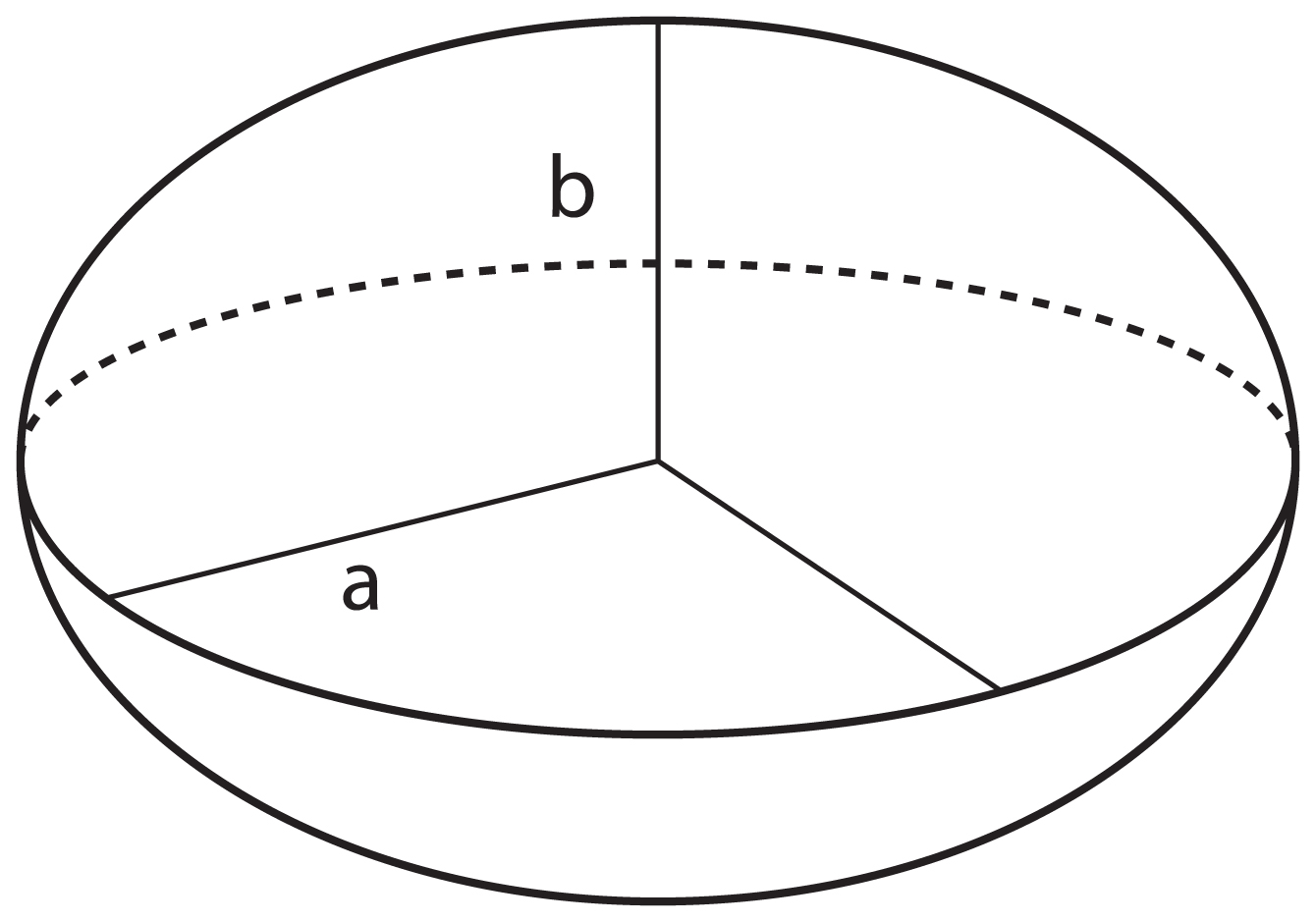
The Earth as a Sphere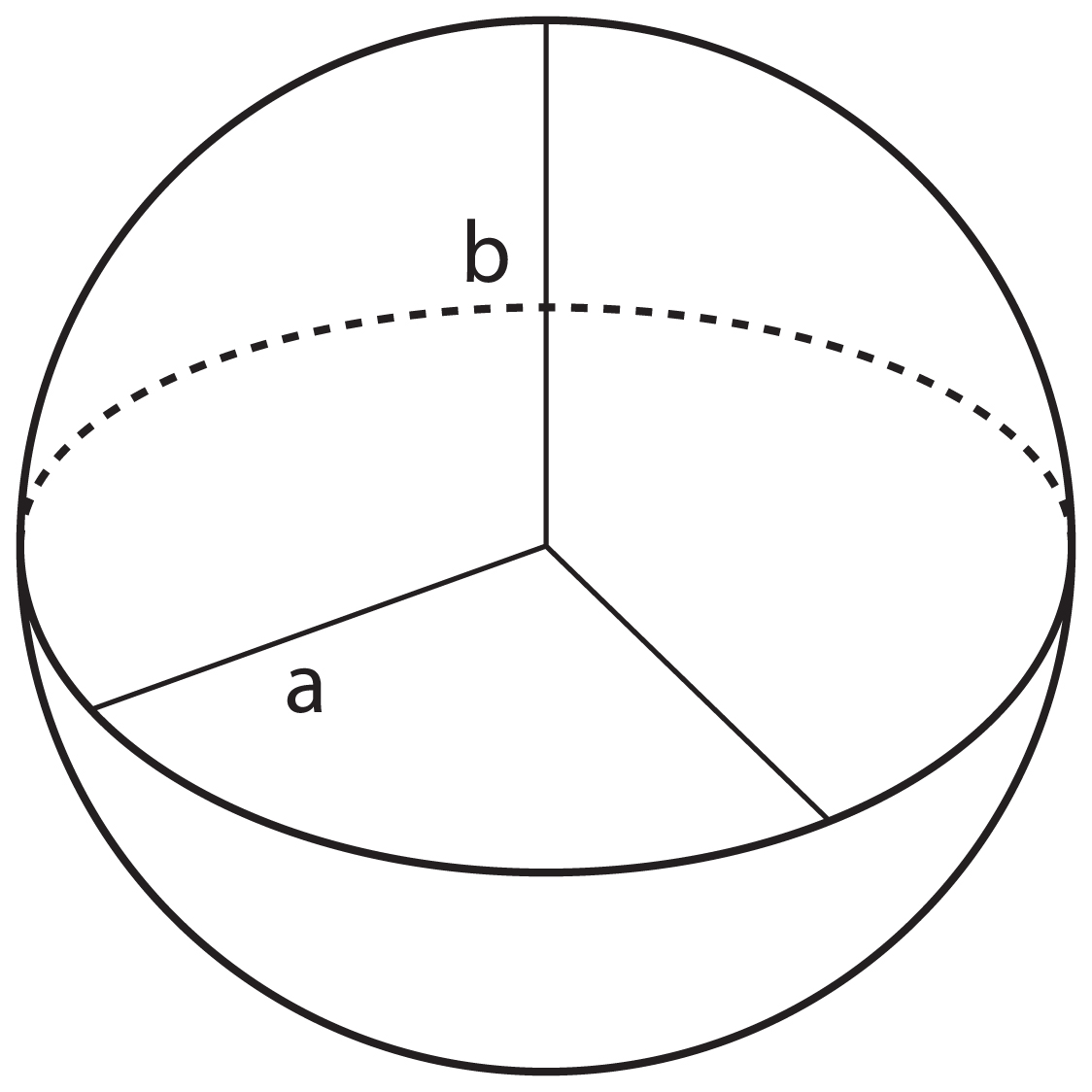
In this calculation the Earth is viewed as being an evenly round ‘ball’. This is called a Sphere.
From an imaginary centre of the Earth, calculations are made from the centre of the Earth to the surface of the Earth.
In this diagram the distances from the centre of the Earth to the Equator and the Geographic ⁄ True North Pole (indicated by ‘a’ and ‘b’) are the same value.
The Earth as an Ellipsoid (or Spheroid)
However, the Earth is not evenly round — it is in fact wider around the Equator than it is between the North and South Poles.
This is called an Ellipsoid (or a Spheroid). All Ellipsoids ⁄ Spheroids are ‘wider’ than they are ‘tall’.
In this diagram the length of ‘a’ is greater than the length of ‘b’.
The Earth as a Geoid
However, this is also a very simplistic concept. The Earth in reality is a very misshapen object. This is called a Geoid.
The Earth’s Geoid is a surface which is complex to accurately describe mathematically. But it can be identified by measuring gravity.
The Earth’s Geoid is regarded as being equal to Mean Sea Level. Over open oceans the Geoid and Mean Sea Level are approximately the same, but in continental areas they can differ significantly. However, it must be noted that this difference it is not of any practical consequence for most people and it is considered reasonable that they are regarded as the same.
Because of the Earth’s Geoid’s irregularity Geodesists have chosen to use Ellipsoids (or Spheroids) to calculate the location of latitude and longitude.
The Earth’s True Shape - Its Terrain
Of course the Earth isn’t just ocean (Mean Sea Level). Much of the land masses are well above the sea level (eg Mount Everest is over 8,000 metres above Mean Sea Level), while in the ocean it is well below sea level (eg the Mariana Trench is over 10,000 metres below Mean Sea Level.
For more information see the section on Elevation in the sections on Cartographic Considerations and Datums explained in more detail.
How These Relate to Each Other
In summary - there are four surfaces that geodesists study:
» the Ellipsoid/Spheroid
» the Geoid
» Mean Sea Level
» the Terrain
It is important to recognise that the relationship between these four surfaces is not always the same. Rather, as this diagram indicates, they ‘wobble’ around each other.
(Please note that for this diagram the relationship between these four has been exaggerated so that you may better understand the nature of this ’wobbling’.)
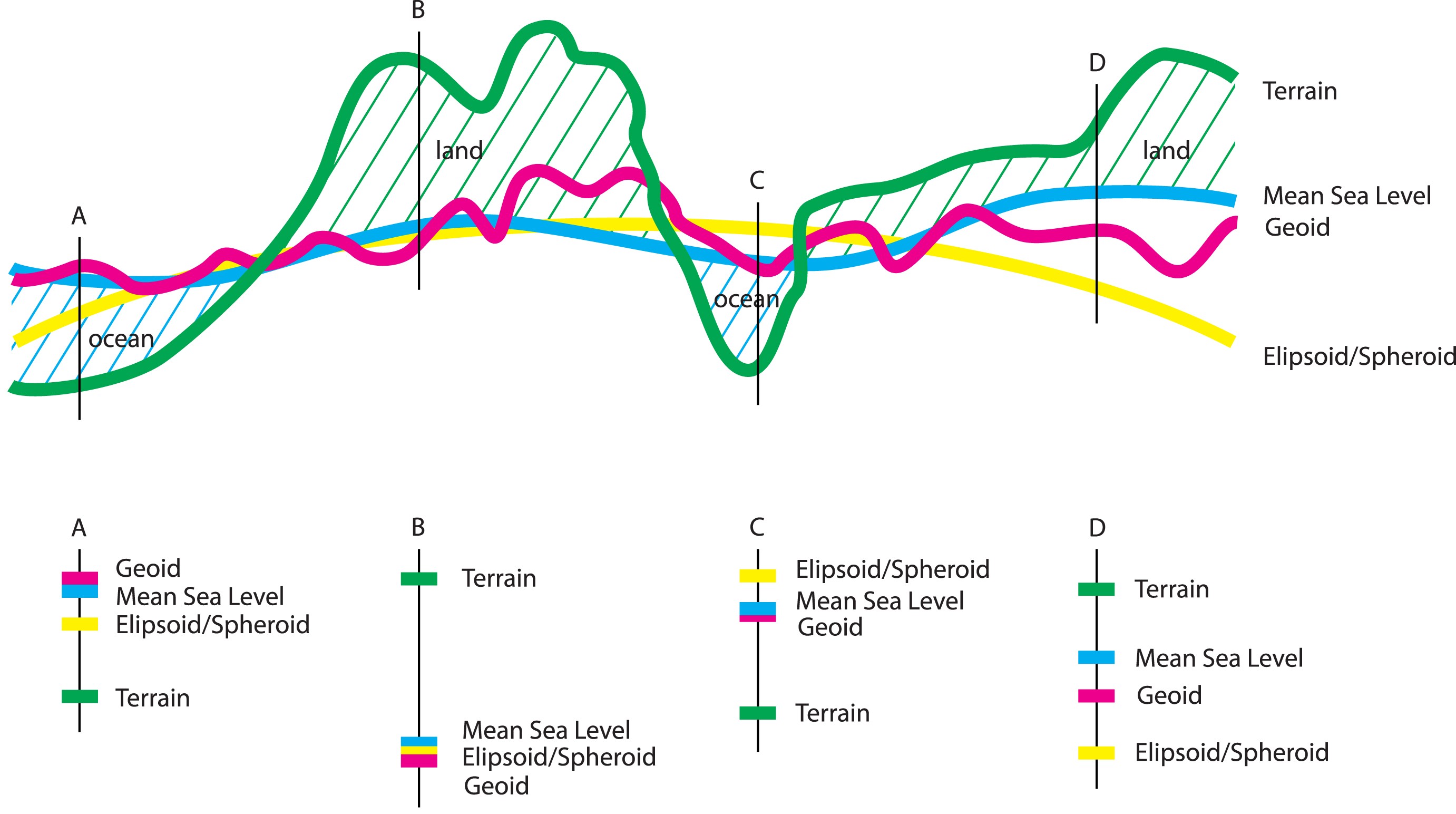
Four examples (A, B, C and D) have been chosen to describe how these relationships may change.
A and C show the Earths’ terrain as being below Mean Sea Level — this is equivalent to an area of ocean. Note how the Geoid and Mean Seal Level are very close to the same value, but their relationship to the Ellipsoid/Spheroid varies.
B and D show the Earths’ terrain as being above Mean Sea Level — this is equivalent to an area of land. It is worth noting that the differences between the Geoid and Mean Seal Level is much greater than in the ocean examples. And, similarly, their relationship to the Ellipsoid/Spheroid varies.
With an understanding of these four geometric shapes and their relationships to each other it is possible to better understand Datums.
Explaining some Jargon — What is Geodesy
Because people who measure the shape of the Earth generally refer to the Earth as a Geoid, the following terms have been developed:
- geodesy
the study of the shape of the Earth and the determination of the exact position of geographical points
(latitude, longitude and elevation) - geodetic
an activity relating to geodesy - geodesist
a person undertaking geodetic work.
A Commonly Asked Question
"What is a geocentric datum and why do we need to use one?"
Because the Earth is so misshapen, when creating a datum to suit their country/region, geodesists have traditionally ’positioned’ the Ellipsoid/Spheroid so that it best matched the Geoid over their country. These are commonly called Local or Regional Datum. (AGD was a regional datum for Australia.)
The result of the use of Local Datums was that lines of longitude and latitude between different countries/regions would not connect evenly. These mismatches were commonly over 100 metres — no big deal in the non–digital era, but with the arrival of the very popular Global Positioning System (GPS) technology this disagreement was no longer acceptable. World-wide datums which would be used in all countries ⁄ regions began to be developed. These are commonly called Geocentric Datums.
These two diagrams illustrate these two situations:
Local or Regional Datums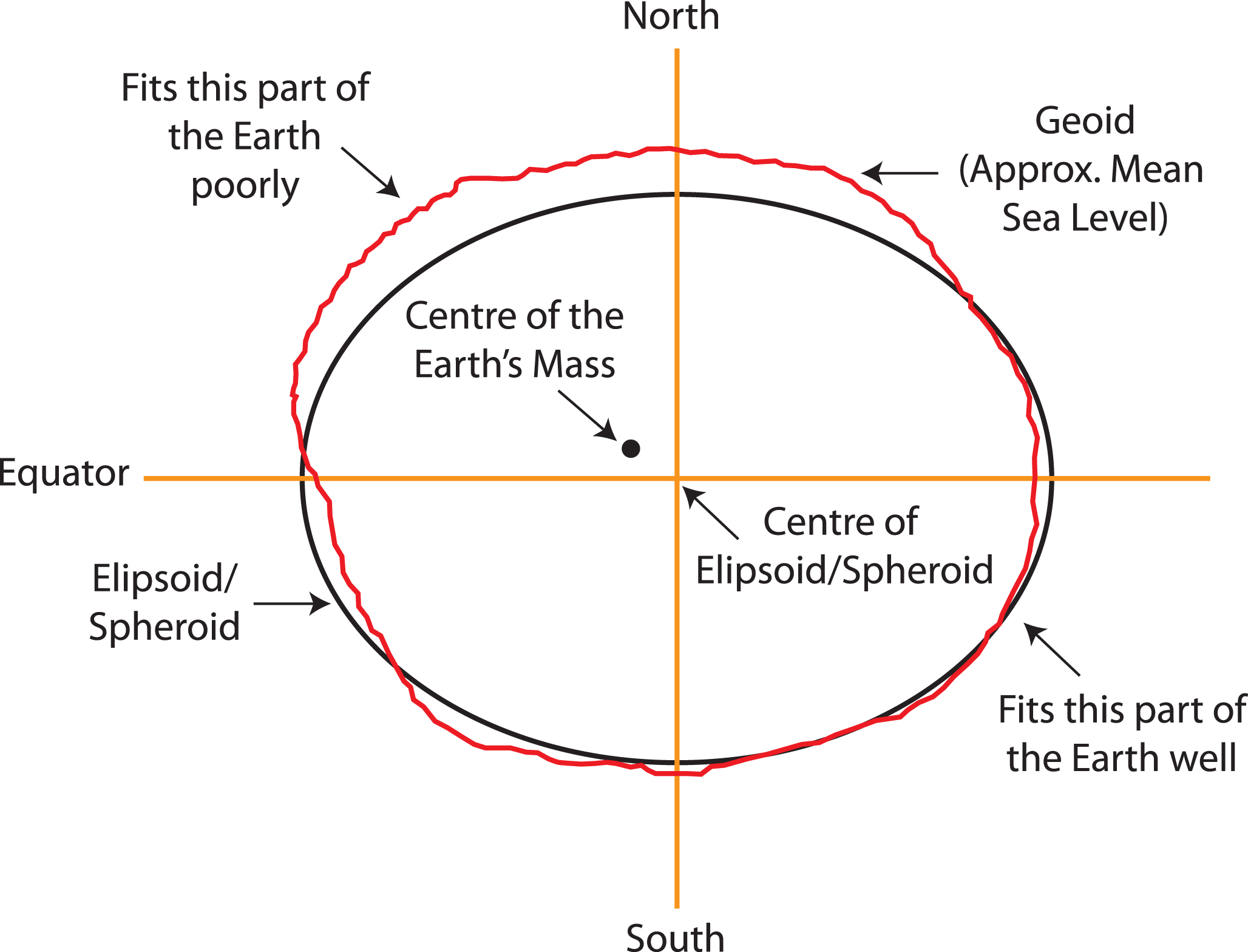
This diagram represents the Australian Geodetic Datum which was created in 1984 (AGD84 or AGD).
Note how the Ellipsoid ⁄ Spheroid has been ’placed’ over Australia to best identify longitude and latitude. If you used this datum in the northern hemisphere longitude and latitude would be very poorly identified on the surface of the Earth.
Geocentric Datums
This diagram represents the Geocentric Datum of Australia which was created in 1994 (GDA94).
This datum was part of a world-wide datum which was compatible with the USA Global Position System (GPS).
Note how the agreement with the Geoid is more even over the whole of the Earth and that the centre of the Earth is also the centre of the Ellipsoid ⁄ Spheroid. This is an essential part of a Geocentric Datum because they are designed for use with Global Position Systems; and their satellites which orbit around the Earth’s central mass.